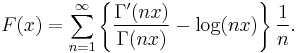Herglotz–Zagier function
In mathematics, the Herglotz–Zagier function, named after Gustav Herglotz and Don Zagier, is the function
introduced by Zagier (1975) who used to obtain a Kronecker limit formula for real quadratic fields.
References
- Herglotz, G. (1923), Berichte über die Verhandlungen der Königlich-Sächsischen Gesellschaft der Wissenschaften zu Leipzig, Mathematisch-Physische Klasse 75: 3–14
- Masri, Riad (2004), "The Herglotz–Zagier function, double zeta functions, and values of L-series", Journal of Number Theory 106 (2): 219–237, doi:10.1016/j.jnt.2004.01.004, ISSN 0022-314X, MR2059072
- Zagier, Don (1975), "A Kronecker limit formula for real quadratic fields", Mathematische Annalen 213: 153–184, doi:10.1007/BF01343950, ISSN 0025-5831, MR0366877